[논문] Improving Calibration for Long-Tailed Recognition
업데이트:
1. Introduction
CVPR 2021에서 발표된 “Improving Calibration for Long-Tailed Recognition”은 학습 데이터에서 각 클래스간의 불균형이 야기하는 문제를 다룬 논문입니다. 최근 이 불균형 문제를 해결하기 위해서 모델 학습을 2단계로 나눠서 진행하는 방법이 이용되곤 합니다. 이 논문도 이 2 stage 학습을 이용하는 논문인데, 이들은 이런 방법에도 불구하고 miscalibration이 있다 주장하며, 새로운 label-aware smoothing 방식을 제안합니다. 저자는 예측의 확률이 각 클래스의 데이터의 수에 크게 연관이 있다는 점에서 착안하여 제시된 label-aware smoothing을 통해 특정 클래스에 대한 과도한 confidence를 줄이고, 이를 통해 classifier의 성능을 개선하고자 합니다.
이 논문에서 자주 등장하는 classifier re-training(cRT)과 learnalble weight scaling(LWS)는 Kang et al.에서 제시된 two-stage decoupling 모델로 이후의 이해를 위해 간략하게 설명하자면 다음과 같습니다.
-
Classifier Re-training(cRT): 불균형을 해결하는 가장 직관적인 방법으로, 불균형 학습 데이터의 클래스간 균형을 맞추어서 모델을 다시 학습시키는 것입니다.
-
Learnable Weight Scaling(LWS): cRT는 데이터의 sampling을 통해 불균형을 해결하고자 한다면, LWS는 representation과 classifier weight를 고정시키고, scaling factor $f_{i}$를 학습하는 것입니다. 이 말을 좀 더 풀어서 쓰자면, 각 class $i$에 대한 classifier $w_{i}$는 그대로 유지를 하되, 이 $w_{i}$가 얼마만큼의 영향력(magnitude)을 갖도록 할지 학습하는 것인데 이 학습하고자하는 magnitude가 scaling factor $f_{i}$입니다.
Calibration?
그외에 제목에 나와있는 calibration을 이해하보자면, 모델의 출력값이 실제 confidence를 반영하도록 만드는 것 입니다. 예를 들어 input $x$의 $y_{i}$에 대한 모델의 출력이 0.8이 나온 경우, 80%의 확률로 $y_{i}$라는 의미를 갖도록 만드는 것 입니다. 만약 모델이 실제 confidence를 반영하도록 학습되었다면 실제 accuracy와 confidence가 같아야 하지만 일반적으로 현대의 딥러닝은 over confident하다 합니다. 이것이 중요한 이유는, 실제로 인공지능 모델을 현실에서 이용할때 모든 판단을 모델이 하지는 않습니다. 예를 들어 false negative가 치명적인 의료 이미지에서 어떤 이미지가 암이다/아니다를 판별할 때 이 모델이 ‘암이 아니다’라고 판단한 이미지 중 그 confidence가 낮은 이미지만 사람이 다시 확인하는 방식으로 진행을 할 수 있는데, 이 경우에 모델이 갖는 confidence가 calibrated된 confidence야 이 모델이 도출한 결과값과 이 프로세스를 신뢰할 수 있습니다.
\[ECE = \sum^{B}_{b=1} {|\mathcal{S}_{b}| \over N} \left| \mathrm{acc}(\mathcal{S}_{b}) - \mathrm{conf}(\mathcal{S}_{b}) \right| \times 100\%\]그래서 이 논문에서는 모델의 confidence가 calibrated된 것인지를 측정하는 수치로 Expected Calibration Error (ECE)를 이용합니다. ECE는 confidence와 실제 accuracy의 차이의 기대값으로, binning을 통해서 위의 식처럼 approximation됩니다. ECE는 B개의 bin에 대해서 각각의 bin마다 정확도의 기대값과 confidence의 차이를 weighted mean한 것입니다. (Calibration에 대한 추가적인 설명은 이곳을 참조하시길 바랍니다.)
Problems
이 논문에서 제시한 해결하고자 한 첫번째 문제점은 long-tail 데이터 셋에서 network는 miscalibtrated되었으며 over-confident하다는 것입니다. 이들은 이를 아래의 그림을 통해서 해당 문제점이 있다는 것을 보여주고 있습니다.
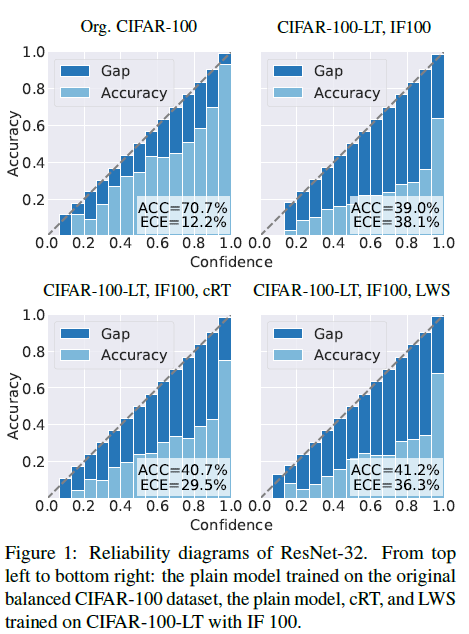
이 이미지는 원본 CIFAR-100 데이터로 학습된 모델과 CIFAR-100-LT를 이용하여 Cross-Entropy로 학습된 모델, cRT로 학습된 모델, LWS로 학습된 모델 이렇게 4가지를 비교하였습니다. 이를 통해 long-tailed dataset이 평균적으로 더 높은 ECE 값을 지니며 cRT와 LWS로 학습된 모델이 over-confidence 문제가 있다는 것을 제시합니다.
두번째 문제점으로는 two-stage decoupling이 이 두 단계 사이의 dataset bias나 domain shift를 무시한다는 점입니다. 예를 들어 stage 1에서 instanced-balanced dataset \(\mathcal{D}_{I}\)로 학습을 한 다음, stage 2에서는 class-balanced된 \(\mathcal{D}_{C}\)로 학습을 하는 경우 두 데이터의 분포는 다릅니다. 따라서 이들은 이 분포가 다른 문제점을 batch-normalization 레이어에서 해결하는 방안을 제시합니다.
Contribution
이들은 총 4가지를 자신의 contribution이라 제시합니다.
-
Long-tailed dataset이 balanced dataset으로 학습된 모델 보다 더 miscalibrated되어있고 over-confident함과 two-stage에서 발생하는 문제 또한 발견하였다.
-
Mixup이 over-confidence를 완화하며, representation 학습에 좋은 영향을 주지만 classifier learning에는 부정적인 영향을 줌을 발견하였다. 그래서 classifier의 성능과 calibration을 개선하기 위해 새로운 label-aware smoothing 방식을 제안했다.
-
두 단계 사이의 dataset bias나 domain shift에 대해서는 처음 다루고 있으며 이를 해결하기 위해서 batch normalization layer에서 shift learning을 제안한다.
-
MiSLAS를 여러 benchmark dataset에 대해서 실험해 보았으며 SOTA에 해당하는 성능을 보였다.
2. Related Work
Re-sampling and Re-weighting
일반적으로 imbalance를 해결하기 위해서 re-sampling과 re-weighting을 많이 이용합니다. Re-sampling은 oversampling, smote, deferred-resampling과 같이 다양한 방식이 있는데, 간단하게 불균형한 데이터들을 직접 조작하여 불균형을 해소하고자 하는 방법입니다. Re-weighting의 경우 데이터 조작이 아닌, 학습시에 각 class마다 다른 weight를 부여하여 imbalance를 해소하는 방식입니다.
Confidence calibration and regualrization
위의 Calibration?에서 많은 설명이 있었으므로 여기서 calibration에 대한 설명은 생략하겠습니다.
Regularization의 방법으로는 lable smoothing이나 data augmentation을 이용하는 등의 방법이 있습니다. 이 논문에서는 기존에 regularization에 도움이 된다는 mixup을 활용하고 label smoothing을 통해 좀 더 개선된 성능을 보이고자 하는 것 같습니다.
Two-stage methods
저자가 DRS와 DRW도 two-stage 라고 하는걸 보았을 때, 모델을 학습시킬 때 학습 중간에 다른 method를 추가하는 식의 방식도 two-stage에 해당되는 것 같습니다. DRS와 DRW 모두 어떤 기법도 적용하지 않은채로 학습을 진행하다, 어느 정도 epoch이 지난 이후 (ex. 160 epoch) learning rate를 바꾸고 oversampling 또는 re-weighting을 적용하여 학습을 시키는 방식입니다. 이렇게 학습 중간에 다른 방법이 적용 된 것을 two-stage method라 한 것 같습니다.
3. Main Approach
3.1. Study of mixup Strategy
Mixup이 두 개로 나눠진 stage에서 어떤 영향을 미치는지 확인하고자 ImageNet-LT에 대해서 실험을 진행하였습니다. Stage 1은 총 180 epoch, stage 2는 총 10 epoch으로 Table 1은 mixup이 적용되고/안되고의 경우에 대해서 실험을 돌린 결과입니다.
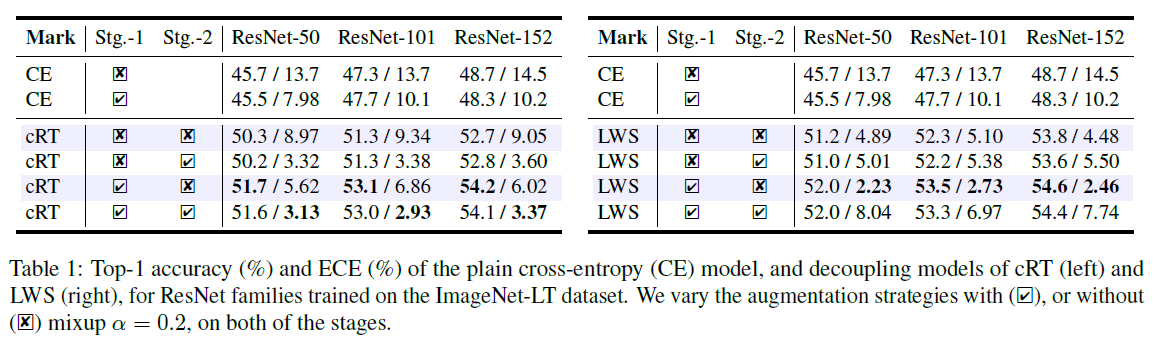
위의 실험 결과를 통해서 저자들은 총 2가지를 알 수 있다 말합니다.
- Mixup이 적용되는 경우, plain cross entropy (CE)의 효과는 무시될 수 있지만, cRT와 LWS에서는 성능이 매우 향상되었다.
- Mixup을 두 번째 stage에 적용하는 경우에는 뚜렷한 성능의 향상이나, 심지어는 저하도 나타나지 않았다.
이러한 이유에 대해서는 mixup이 representation learning을 촉진시키고, 아직 classifier 학습에 역효과, 또는 미미한 효과를 갖지 때문이라 말합니다.
성능 외에도, calibration의 정도를 비교하기 위해서 ECE의 값도 측정이 되어있습니다. ECE 값을 비교해보면, cRT와 LWS 모두 mixup을 stage-1에만 적용한 경우의 성능이 더 좋은 정확도와 낮은 ECE 값을 얻어냄을 확인할 수 있었습니다.
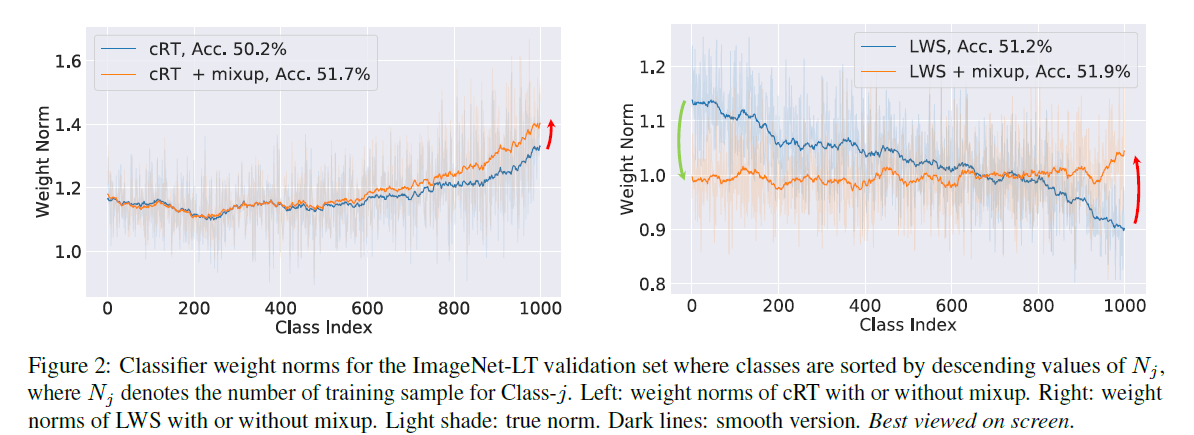
그 외에도 figure 2에서 final classifier의 weight norm을 보여주는데, 여기서 mixup이 적용된 경우를 보면 (주황색) tail class에 대한 weight가 커지고, head class에 대한 weight가 감소한 것을 관찰할 수 있습니다. 이 효과는 LWS에서 더욱 극명하게 드러나며, 이것은 mixup이 tail class에게 더 좋은 효과를 갖는 것이라 말할수 있습니다.
이러한 결과들을 바탕으로 Mixup이 성능 향상에도 도움을 주며, 특히 ECE 값을 낮추는데에 많은 효과를 보였음을 확인할 수 있었습니다.
3.2. Label-aware Smoothing
Stage-1에서는 앞서 설명된 mixup을 적용하였다면, stage-2에서는 label-aware smoothing을 적용합니다. 저자들은 label-aware smoothing을 통해서 두가지의 문제를 해결하고자 했는데, 첫번째는 over-confidence이고 두번째는 limited improvement입니다.
일반적인 cross-entropy를 사용하면 over-confidence와 예측된 확률마다 그 분포가 다르다는 문제가 발생합니다. 이를 해결하기 위해서 아래와 같은 label-aware smoothing 방식을 제안합니다.
\[l(q, p) = -\sum^{k}_{i=1} q_{i} \log p_{i}, \\ q_{i} = \begin{cases}1 - \epsilon_{y} = 1-f(N_{y}), & i=y, \\ \frac{\epsilon_{y}}{K-1} = \frac{f(N_{y})}{K-1}, & \mathrm{otherwise,} \end{cases}\]$\epsilon_{y}$는 class $y$에 대한 smoothing factor이며, class의 데이터 양 $N_{y}$와 연관되어 있습니다. 이것에 대한 최적의 solution은 아래의 식과 같이 되며, $c$는 임의의 실수입니다.
\[w_{i}^{*\top} x = \begin{cases} \log\left( \frac{(K-1)(1-\epsilon_{y})}{\epsilon_{y}} \right)+c, & i=y, \\ c, & \mathrm{otherwise,} \end{cases}\]Cross entropy와 비교하였을때, label-aware smoothing은 overfitting을 완화하는 최적의 해결책입니다. 아래의 식은 3가지의 다른 related function $f(N_{y})$를 보여줍니다.
- Concave
- Linear
- Convex
$\epsilon_{1}$과 $\epsilon_{K}$는 hyperparameter이며, 각 3개의 성능 차이는 후에 experiment의 figure 6에서 나타납니다. 이 label-smoothing이 실제로 효과가 있는가?에 대한 결과는 figure 3을 통해서 확인할 수 있습니다. Head는 각 클래스의 데이터가 100+인 경우, medium은 20~100개, 그리고 tail은 20개 보다 적은 경우입니다. 각 이미지에서 위쪽의 light blue는 label-aware smoothing이 적용되지 않은 경우인데 head와 medium에서 그 결과가 상당히 over-confident함을 확인할 수 있습니다. 반면에 label-aware smoothing을 적용한 경우에는 head와 medium에서의 over-confidence가 많이 해소되었으며 특히 tail에서는 전체적으로 낮은 predicted probability가 약간 상승했음을 확인할 수 있었습니다.
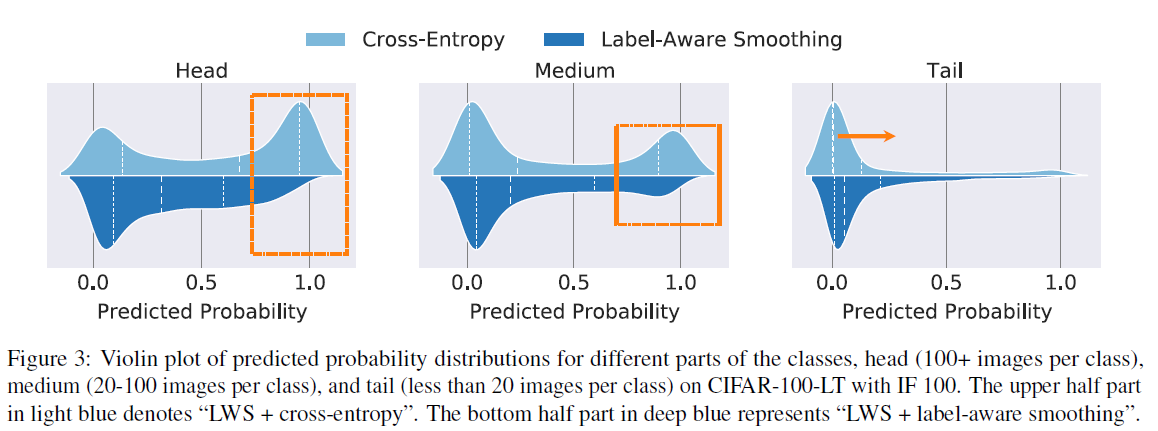
이 label-aware smoothing 방식 자체가 복잡하다보니, 저자들은 보다 일반화된 classifier learning framework를 제안했습니다. cRT와 LWS를 간단하게 되짚어 보면, cRT는 학습 가능한 파라미터가 많고, LWS는 더 나은 validation loss와 성능을 보입니다. 즉 cRT는 더 좋은 표현력을 지니고, LWS는 일반화 능력이 좋습니다. 이러한 장점들을 합쳐서 이 논문에서는 아래의 식과 같은 classifier framework를 만듭니다.
\[z = \mathrm{diag}(s)(rW+\triangle W)^{\top}x.\]위의 식은 original classifier의 가중치 $W$를 고정시킵니다. 만약 learnable scaling factor $s$를 고정시킬 경우, $s=1$로 설정하고, retention factor $r=0$으로 설정합니다. 그리고 새로운 classifier의 가중치 $\triangle W$만을 학습합니다. 위의 식은 cRT는 새로이 classifier의 weight를 학습하고, LWS는 scaling을 학습한다는 점을 동시에 적용할 수 있게 합니다.
3.3. Shift Learning on Batch Normalization
하지만 two-stage의 stage-1에서 모델은 instance-balanced sampling으로 학습된 반면, stage-2에서는 class-balanced sampling으로 학습이 되었습니다. 이 \(\mathcal{D}_{I}\)는 \(\mathcal{D}_{C}\)는 서로 다른 데이터 셋이라 할 수 있기 때문에 이를 transfer learning의 한 종류라 말할 수 있습니다. 이 학습 과정을 transfer-learning의 관점으로 본다면, backbone을 그대로 고정시킨채로 classifier만 tuning하는 것은 잘못되었다 할 수 있습니다. 그래서 저자들은 batch normalization layer에서 shift learning을 할 것을 제안합니다. \(\mathcal{D}_{I}\)와 \(\mathcal{D}_{C}\)이 지니는 mean과 variance가 다르기 때문에 각각에 stage에서 다른 mean과 variance를 적용하여 batch normalization을 적용할 수 있도록 합니다.
4. Experiments
4.1. Dataset and Setup
4.1.1 Dataset
실험에 사용된 데이터 셋은 imbalance task에서 대표적인 CIFAR-LT, ImageNet-LT, Place-LT 그리고 iNaturalist 2018 데이터 셋입니다. CIFAR-LT는 원본 CIFAR 데이터 셋에서 imbalance factor에 따라서 그 불균형의 정도를 조정하여 사용하는 데이터 셋입니다. 이 논문에서는 불균형의 정도가 100, 50, 그리고 10인 경우에 대해서 실험이 진행되었습니다. ImageNet-LT도 마찬가지로 원본 ImageNet 데이터에서 선별된 이미지만으로 모델을 훈련시키며 약 115.8K 이미지가 1,000개의 class로 부터 선택되었습니다. Class 불균형의 정도는 5개의 이미지만 있는 클래스 부터 1,280개입니다. Place-LT는 large-scale scene classification에 이용되는 데이터 셋의 long-tail 버전입니다. Place-LT는 약 184.5K 이미지가 365개의 class로 부터 선택되었으며 불균형의 정도는 5개의 이미지만 있는 클래스 부터 4,980개입니다. 마지막으로 iNaturalist 2018은 이미지 분류 데이터이며 원본 데이터 자체가 극심한 불균형을 지니고 있습니다. 총 437.5K 이미지를 지니고 있고 8,124개의 클래스로 이루어져 있습니다. 또한 2018 데이터 셋에서는 fine-grained problem 또한 나타납니다.
4.1.2 Implementation Details
- Optimizer: SGD momentum 0.9
- Model structure
- CIFAR-LT: ResNet-32
- ImageNet-LT, Place-LT, iNaturalist 2018: ResNet-10, 50, 101 and 152
- Learning Rate
- CIFAR-LT: Follow Cao et al.
- ImageNet-LT, Place-LT, iNaturalist 2018: Follow Kang et al.
4.2. Ablation Study
논문에서 주장한 contribution이 실제로 타당한지, 아래의 실험들을 통해 확인할 수 있습니다.
Calibration Performance
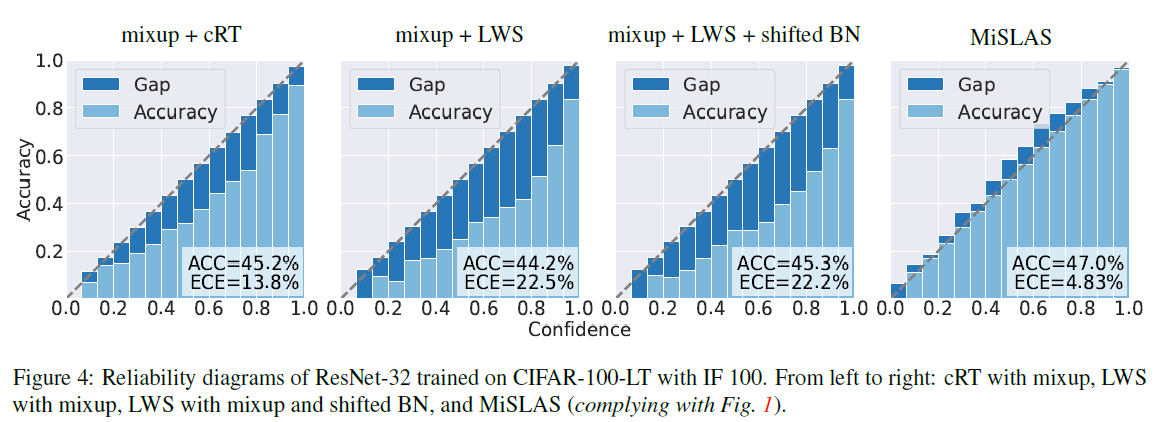
먼저 실제로 논문에서 제안한 MiSLAS가 calibration performance에 영향이 있었는지 확인해보고자 합니다. 아래의 figure 4의 MiSLAS를 다른 3개의 결과와 비교했을때, 실제로 그 효과가 있었음을 보입니다. 3번째와 4번째 결과의 비교를 통해서 label-aware smoothing이 calibration 성능의 개선에 상핟한 효과가 있었음을 확인할 수 있습니다.
Re-weighting 과 label-aware smoothing(LAS) 비교
사실 label-aware smoothing도 re-weighting의 한 종류 입니다. 그래서 실험을 통해 기존의 re-weighting보다 더 나은 점을 보여주고자 합니다. 기존의 Re-weighting 기법 중에도 Class간의 균형을 기준으로 re-weighting을 하는 방식이 있는데 table 2는 기존의 기법과의 비교를 통해 정확도와 calibration 모두에서 그 성능이 더 좋음을 보여주고 있습니다.
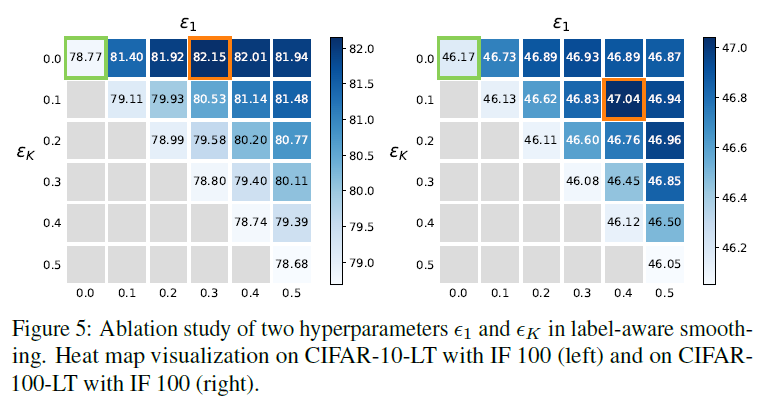
\(\epsilon_{1}\)과 \(\epsilon_{K}\)가 LAS에 미치는 영향
저자는 \(\epsilon_{1}\)과 \(\epsilon_{K}\)의 값을 0.0부터 0.5까지 설정하여 실험을 돌려보았으며 결과적으로 \(\epsilon_{1}=0.4\) \(\epsilon_{K}=0.1\)이 지속적으로 0.9% 좋은 성능을 CIFAR-100-LT에서 보였다고 했습니다.
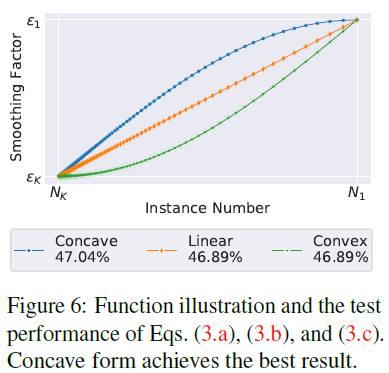
\(f(\cdot)\)이 LAS에 미치는 영향
이는 figure 6에서 확인할 수 있습니다. 이들은 이전 결과들과 마찬가지로 실험을 통해서 Concave의 성능이 가장 좋음을 보였습니다.
요약
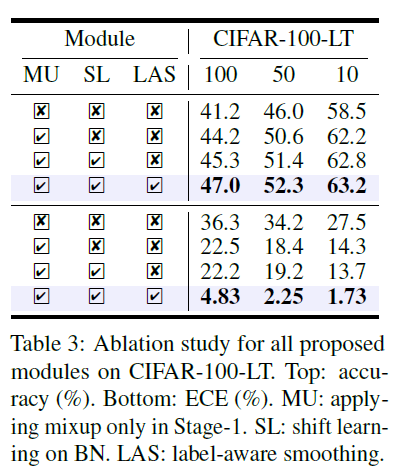
이 표는 MU(MixUp), SL(Shift Learing), LAS(Label-Aware Smoothing)의 각각의 효과를 보여주는 표입니다. CIFAR-100-LT에 대해서 진행된 실험이며 위의 4줄은 정확도, 아래 4줄은 ECE를 보여줍니다. 이를 통해 각 방법이 실제로 성능향상에 도움이 됨을 뒷받침하고 있습니다.
4.3. Comparison with State-of-the-arts
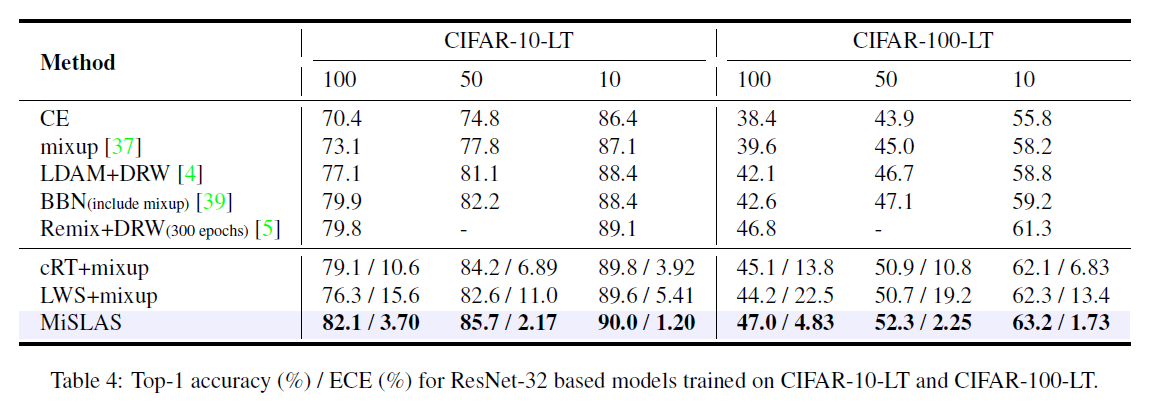
최종적으로 SOTA 기법들과의 비교를 진행합니다. Table 4는 CIFAR-10-LT, CIFAR-100-LT에 대해서 실험을 진행한 결과인데 정확도와 ECE 모두 기존의 방법들에 비해서 더 향상된 성능을 보여주고 있습니다.
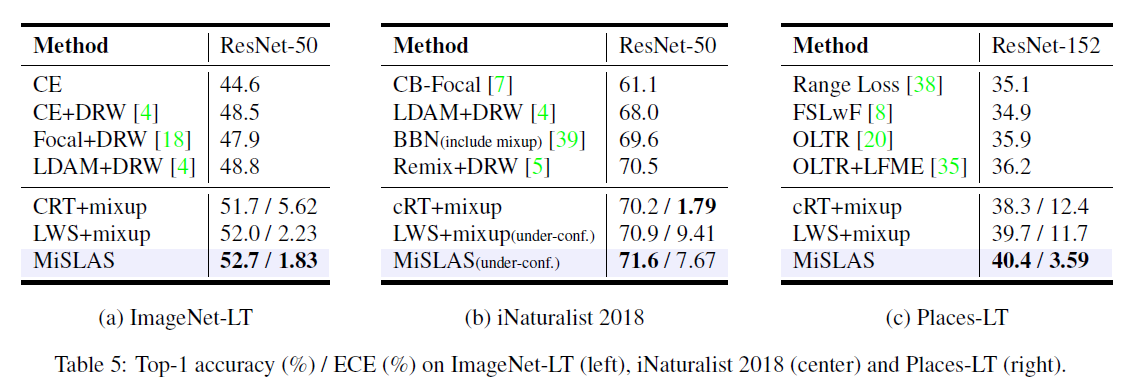
다른 ImageNet-LT, Place-LT, 그리고 iNaturalist 2018에 대해서도 MiSLAS가 좋은 성능을 보임을 table 5에서 확인할 수 있습니다.

댓글남기기