[논문] Towards Deep Learning Models Resistant to Adversarial
업데이트:
1. Introduction
Computer vision과 natural language processing과 같은 분야에 있어서 훈련된 model들은 benign한 input들에 대해서는 아주 높은 정확도를 보이지만, adversarially chosen input에 대해서는 잘못된 결과값은 도출해낸다. 이에 대한 방어를 고려한 설계는 하나의 중요한 목표가 되어가고 있다. 이 논문에서는 우리가 어떻게 하면 deep neural network를 adversarial input에 대해서 robust하게 만드는가 에 대한 이야기를 한다.
How can we train deep neural networks that are robust to adversarial inputs?
이 논문이 나오기 전에도 여러 공격, 그리고 방어에 대한 다양한 방법이 제시 되었었다. 하지만 우리는 그 방법들이 가장 강력한 공격이라고 확신할 수 없고, 반대로 가장 robust한 방어법이라고 보장할 수도 없다.
이 논문에서는 neural network의 adversarial robustness를 robust optimization의 측면에서 본다. 여기서는 saddle point(min-max) formulation을 이용하여 보안성을 보장할 수 있으며 이 formulation은 attack과 defense 모두를 가능하게 한다. 특히 adversarial training을 통해서 가장 최적인 지점(saddle point)을 찾아 다른 공격에 있어서도 robust 할 수 있다고 이야기 한다. 이러한 관점에서 이 논문은 3가지 contribution을 갖는다.
- Saddle point formulation에 잘 최적화 될 수 있는 모델을 만드는 법을 제시한다. (이는 first-order method인 PGD attack을 통해서 해결할 수 있다.)
- Adversarial robustness를 위해서는 capacity가 큰 모델이 필요하다.
- MNIST와 CIFAR-10에 대해서도 높은 정확도를 지녔다.
2. Optimization View on Adversarial Robustness
일반적으로 neural network는 loss값을 계산하여 loss값을 줄이는 방향으로 학습을 한다. Empirical risk minimization도 train error를 최소화 시키는 한가지 방법이다. 하지만, 이 또한 모든 adversarial example에 대해서 robust하지 않다. 실제로 adversarial 공격 중 c1이라는 label을 갖는 data를 아주 근처에 있는 c2라는 label을 갖도록 바꾸는 방식의 공격도 존재한다. 그래서 model을 reliable하게 train하려면 이 ERM 패러다임을 적절하게 변경해야한다. 이것에 대한 첫번째 접근 방식으로는 adversarially robust한 model이 충족해야할 guarantee를 제시하는 것이다.
첫번째 step은 논문에서의 model이 방어해야할 attack model에 대한 정확한 정의를 제시하는 것이다.
이 수식은 loss를 최대로 만드는 adversarial에 대한 loss의 값이 최소가 되도록 학습을 시킨다는 의미이다.
첫째로 이 수식은 이전의 adversarial robustness의 연구에 대한 통합된 관점을 제시한다. 이 관점은 adversarial problem을 saddle point problem으로 보며, 이는 inner maximization problem과 outer minimization problem으로 나뉜다.
- inner maximization problem: 주어진 data \(x\)가 가장 높은 loss를 얻는 adversarial version을 찾는 것
- outer minimization problem: inner attack problem에 의해 주어진 “adversarial loss”가 최소화 될수 있는 model parameter를 찾는 것
둘째로 saddle point problem은 robust한 classifier가 달성해야할 명확한 목표를 제시한다.
2.1 A Unified View on Attacks and Defenses
Adversarial example에 대한 이전의 연구는 두가지 큰 문제에 집중해왔다.
- Attack: 어떻게 하면 적은 변형만이 가해진 강한 공격을 만드는가?
- Defense: 어떻게 하면 적대적 예제가 없거나, 찾기가 힘들게 모델을 train할 수 있는가?
공격의 경우, FGSM(Fast Gradient Sign Method)가 있다. 이는 loss값에 대해서 gradient를 계산하고 gradient의 sign값에 대해 입실론 만큼 이미지를 변경하는 방식이다. 이 논문에서는 같은 \(L_{\infty}\) attack인 project gradient descent(PGD)공격을 이용한다. 이는 매우 강력한 공격방법 중 하나이며, 간단히 말하면 FGSM을 step 단위로 나눠서 사용하는 방식의 공격이다. 그 외의 특징으로, random perturbation이 있는 FGSM의 방식도 제안되었다. 이 모든 접근방식은 inner maximization을 해결하기 위한 접근법으로 보일 수 있다.
- FGSM
- PGD
방어의 경우에는 train dataset을 전부 adversarial dataset으로 대체하여 train하는 방식을 사용한다.
3. Towards Universally Robust Networks
Inner maximization은 loss를 가장 높이는 공격방식을 의미하지만, 이러한 예제 자체가 존재하지 않는다. 그러므로 formulation 2.1이 더 이상 network를 공격할 방법이 없다는 것을 보장한다. 그럼 이제는 2.1에 대해서 좋은 값을 갖는 방식에 대해 알아보자.
이 논문의 주요 contribution중 하나는 saddle point problem을 해결할 수 있다는 점이다. 그 시작으로 non-concave inner problem에 대해 이야기 해보자. 이는 아주 간단한 방식으로 해결할 수 있다.
3.1 The Landscape of Adversarial Examples
Inner problem은 adversarial example을 만드는 것과 동일하다. 이미 FGSM과 같은 공격 방법들이 있으며 FGSM은 상당히 우리가 사용하기 쉬운 방식 중 하나이다. 이런 FGSM을 이용한 adversarially train된 model들이 이미 FGSM과 같이 약한 공격에 대해 robust하다는 것을 보인 논문들이 있다. 이 논문은 그런 연구들을 참조하였다.
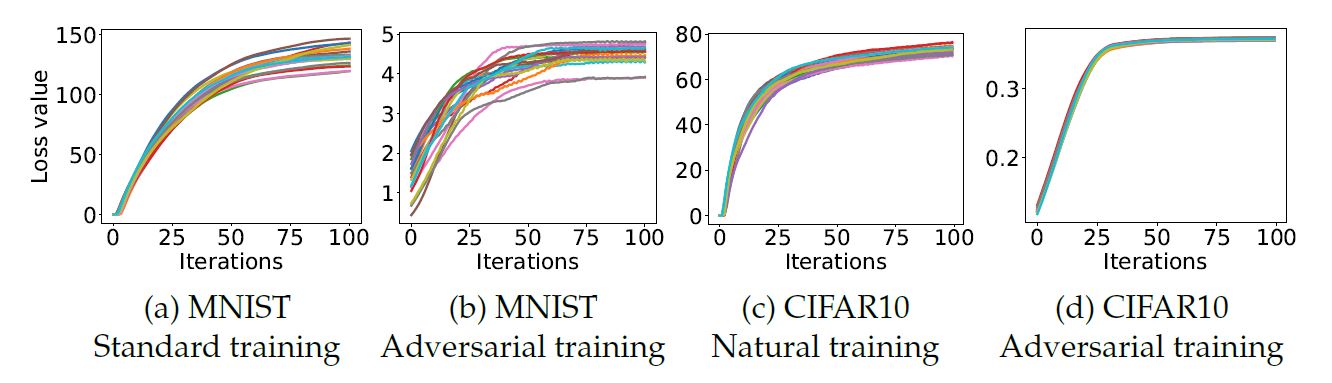
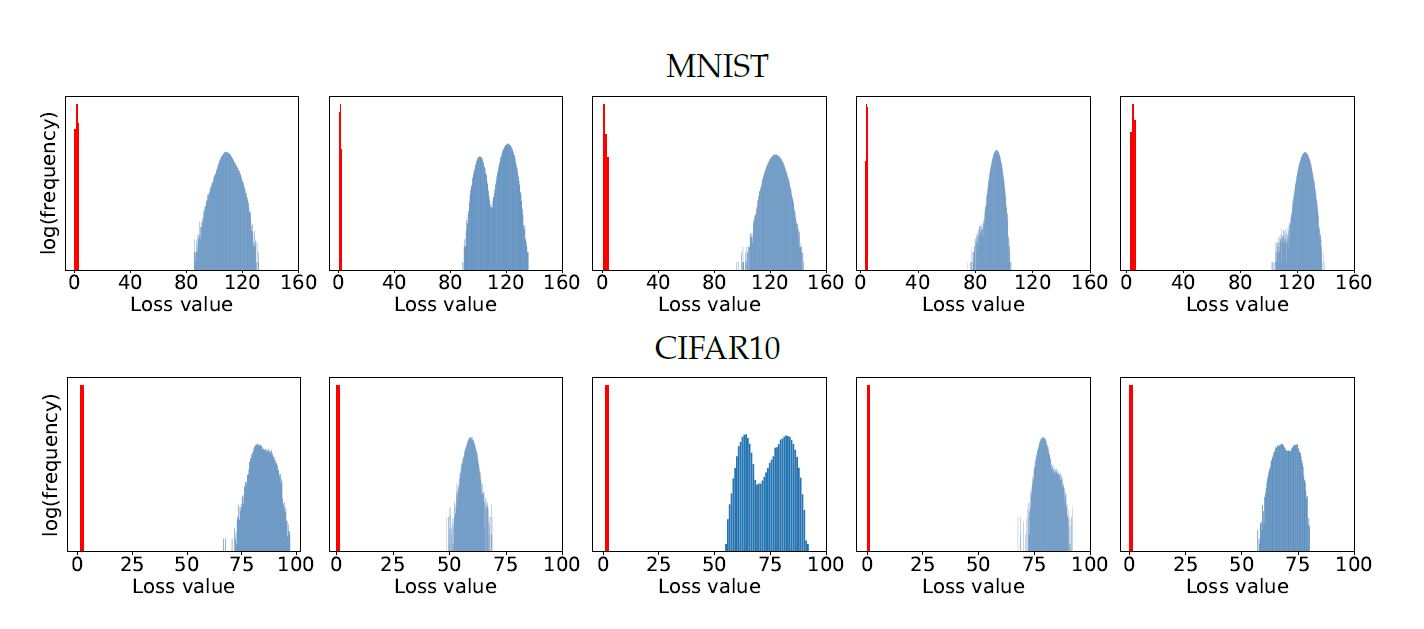
이 논문에서는 MNIST와 CIFAR-10에 대해 PGD attack을 이용하여 adversarial train을 하였고, random point에서 시작을 하였다. 놀랍게도 다양한 random point에서 출발했지만, 결국 만들어진 adversarial example들은 비슷한 loss값을 지니게 되었다. 이는 논문에서 해결하고자 한 min-max formulation을 PGD를 통해서 충족시키는 것이 가능하다는 이야기이다. 아래의 이미지를 통해서 loss값이 비슷한 값으로 수렴하는 것을 관찰할 수 있다. 그 외에도 adversarial training이 된 model의 loss value가 standard training과 비교했을 때, 그 값이 월등하게 작다는 것도 관찰할 수 있었다.
아래의 그림은 cross-entropy loss에 의해서 주어진 local maxima에 대한 값이다. 각각의 MNIST, CIFAR-10에 대해 동일하게 random한 point에서 실행한 결과값들이다. 파란색 히스토그램은 standard network, 빨간색 히스토그램은 adversarial trained network에 대한 결과로 이는 PGD보다 더 loss값을 낮게 만드는 방법은 찾기가 어렵다는 것을 보여준다.
위의 결과값들을 분석해보았을 때, PGD는 굉장히 강력한 first-order approach라 이야기 할 수 있다.
3.2 First-Order Adversaries
이 논문에서의 실험들은 PGD로 만들어진 대부분의 예제들은 비슷한 loss 값을 지니며 이는 PGE를 통해 만들어진 model은 대부분의 first-order adversary에 대해서 robust하다 이야기 할 수 있다. 실제로 실험 결과 PGD 공격보다 더 나은 local maxima를 만드는 공격을 찾기는 어려웠다 이야기 한다. 결론적으로, PGD에 대해서 충분히 robust하다면 다른 attack들에도 충분히 robust할 것이라 이야기한다.
3.3 Descent Directions for Adversarial Training
일반적으로 우리는 SGD에 기반한 minimization 기법을 이용한다. 과연 이런 방식으로 saddle point problem도 잘 해결될 수 있을까라는 의문을 갖는데, Danskin’s theorem에 따라서 연속적으로 미분가능한 함수에서는 학습이 잘 될 수 있을 것이라 이야기한다.
4. Network Capacity and Adversarial Robustness
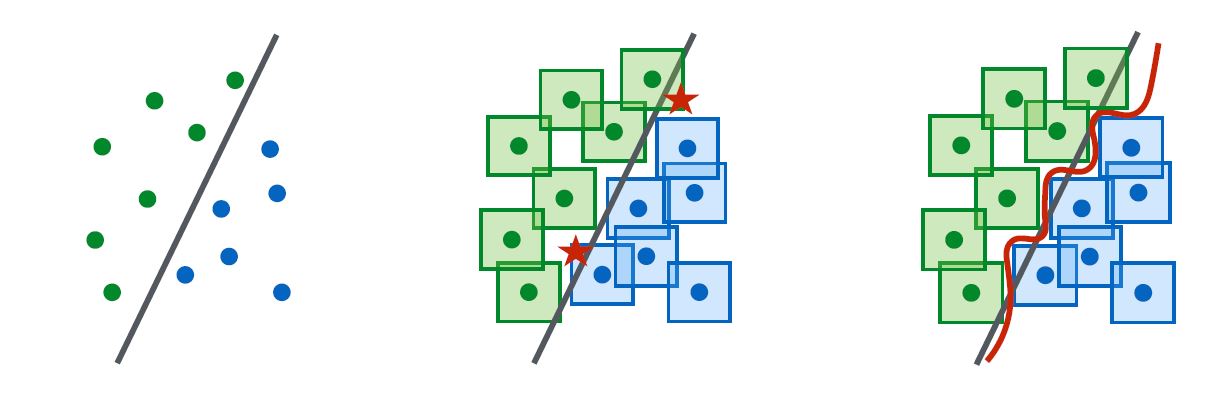
위의 이미지는 standard와 adversarial의 decision boundary 그림이다. 이는 adversarial training을 통해서 epsilon값에 맞춰 model이 non-linear하게 학습됨을 관찰할 수 있다.
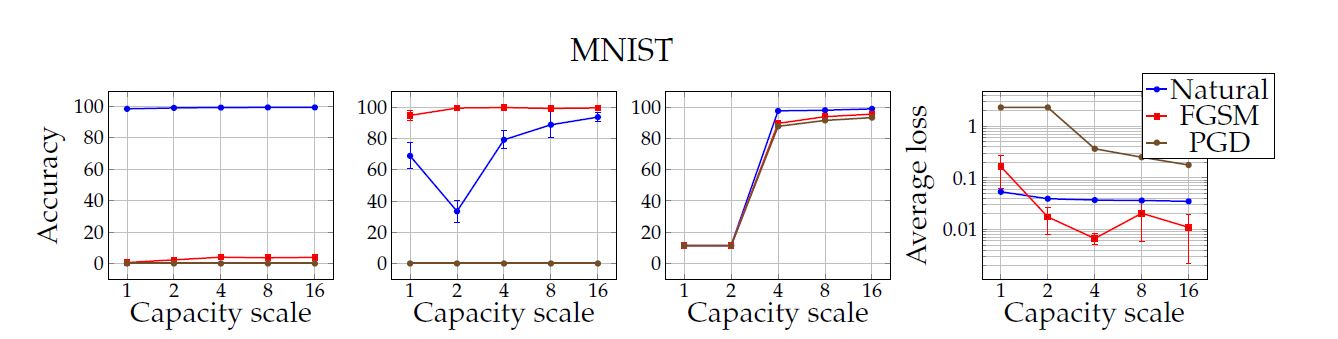
이 논문에서의 실험은 capacity가 robustness에 있어서 아주 중요하며, 강력한 adversary에 대하여 train하는 데에도 중요하다는 것을 보여준다. MNIST dataset에 대하여 아주 간단한 convolution network에 대해 그 크기를 두배씩 키워나가면서 변화를 관찰했는데 결과는 아래와 같았다.
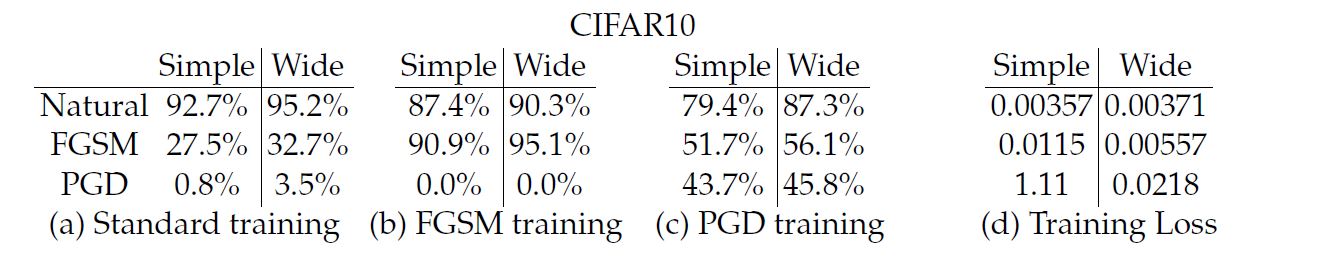
CIFAR-10에 대해서는 ResNet을 이용하였는데, data augmetation을 이용하였으며 capacity를 늘리기 위해서 넓은 layer를 10의 배수로 결합시키도록 변환하였다. 아래는 이에 대한 결과값이다.
위의 실험들을 통해서 몇가지 현상들을 관찰할 수 있었다.
- Capacity만의 증가로도 adversarial training에 도움이 된다.
- FGSM adversary만으로는 robustness를 충분히 증가시킬수 없다. (입실론 값을 증가시킬 경우, label leaking이 발생한다.)
- Capacity가 작으면 adversarial training 자체가 잘 안될 수 있다.
- Capacity를 증가시키면 saddle point problem의 값이 감소한다.
- Capacity의 증가와 강력한 adversary는 transferability를 감소시킨다.
5. Experiments: Adversarially Robust Deep Learning Models
결과적으로 두가지에 집중해야한다.
- network는 충분히 높은 capacity를 가져야한다.
- 강력한 adversary를 사용해야한다.
Figure4에 대해서 결과를 분석하면 MNIST에서는 capacity가 증가하면 정확도가 증가하는 것을 확인할 수 있다. CIFAR-10에서는 FGSM으로 train된 모델에 대해서는 label leaking이 발생하며 PGD에 대해서는 전혀 방어 효과가 없음을 관찰할 수 있었다. 또한 더 wide한 모델에서 정확도가 더 높게 나옴을 관찰할 수 있었다. 그리고 adversary에 대해서 train을 할 때, adversarial exmaple에 대해서 training loss가 살짝 감소하는 것을 확인할 수 있다.
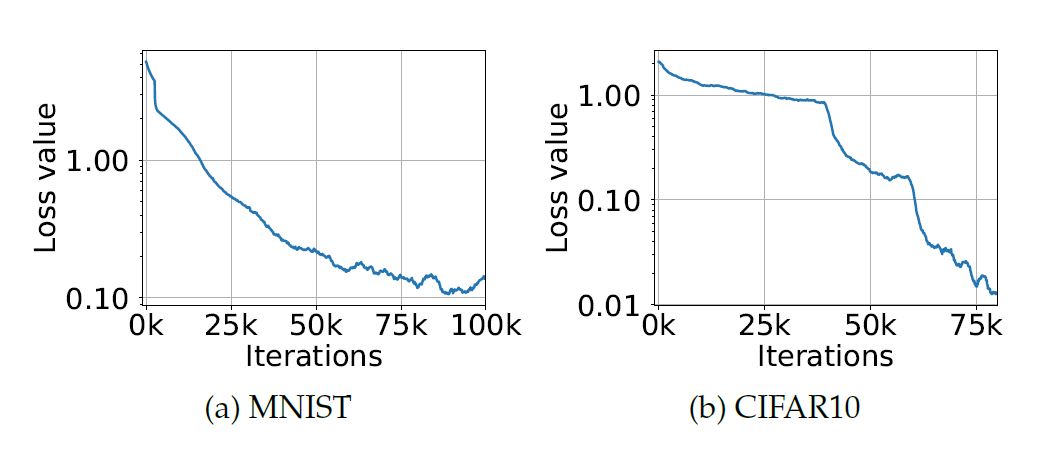
아래 그래프는 training 동안의 cross-entropy loss 값의 그래프이다. CIFAR-10에서의 두번의 급격한 감소는 training step 크기의 감소로 생긴 결과이다.
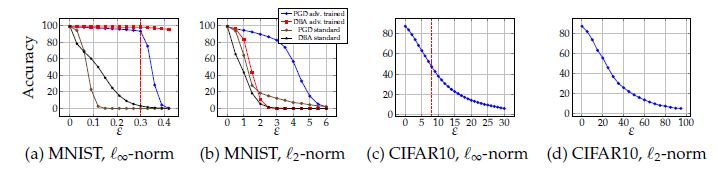
그 외에도 epsilon값을 바꿔가며도 실험을 해 보았고, \(L_{2}\) attack에 대해서도 실험을 해보았다고 한다. Epsilon의 경우 그 값이 조금 증가해도 정확도가 많이 떨어지며, \(L_{\infty}\) attack에 대해서 robust하다면 \(L_{2}\) attack에 대해서 어느정도 robust함을 관찰할 수 있다고 한다.
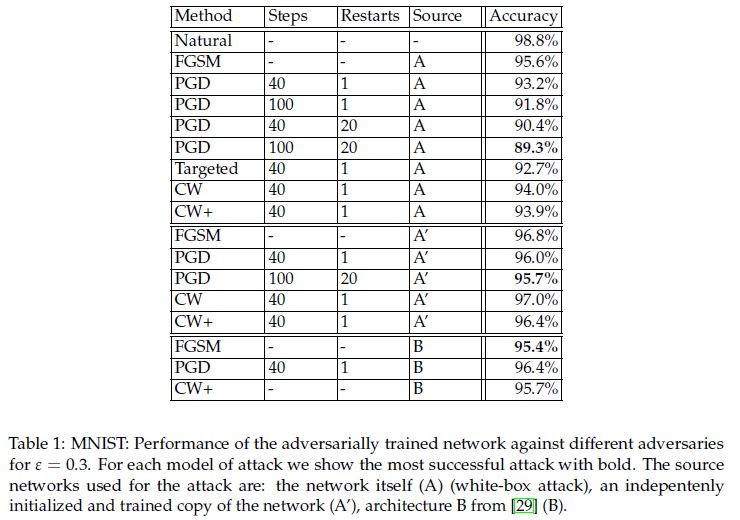
- Table1(MNIST)
강력한 PGD 공격에 대해서도 높은 정확도를 보임을 확인할 수 있었다. 그 외에 구조는 같고 새롭게 학습한 모델에 대해서는 95.7%의 높은 정확도를 갖는것을 볼 수 있었다. 마찬가지로 다른 구조를 갖는 모델에 맞춰진 attack에 대해서도 방어가 잘 되고 있음을 확인할 수 있었다.- A: white box
- A’: 모델의 구조는 같은데 weight는 다름
- B: 구조도 다른 black box
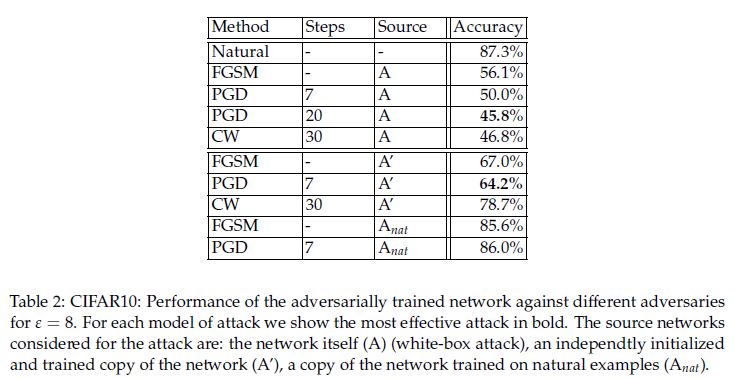
- Table2(CIFAR-10)
마찬가지로 강력한 PGD 공격에 대해서도 45.8의 정확도를 보임을 확인할 수 있었다. 그 외에 구조는 같고 새롭게 학습한 모델에 대해서는 64.2%의 정확도를 갖는것을 볼 수 있었다.- A: white box
- A’: 모델의 구조는 같은데 weight는 다름
- A_nat: natural example로만 train된 모델에 대한 공격
6. Conclusion
강력한 adversarial 공격에도 robust한 모델을 제시하였으며, MNIST 데이터에서는 굉장히 robust하고 높은 정확도를 보였다. CIFAR-10에 대해서는 아직 그정도의 정확도를 이루지는 못했지만, 이 논문의 결과값은 소개된 기술들이 network의 robustness를 증가시켰음을 보여준다.

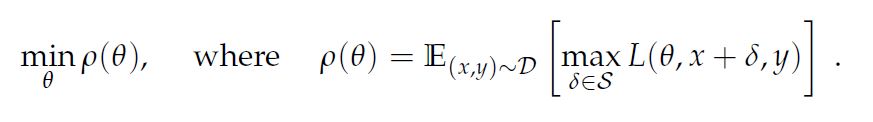
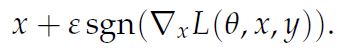
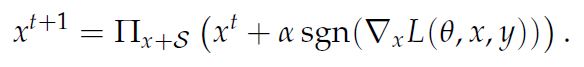
댓글남기기