[논문] Towards Evaluating the Robustness of Neural Networks
업데이트:
Introduction
- Deep neural networks는 많은 machine-learning task에 있어서 효과적이지만, 현존하는 neural network가 adversial example에 취약하다는 것을 발견해냈다. (Szegedy et al, 2013)
- Defensive distillation은 adversarial example에 대응하는 한가지의 방법이다. (Papernot et al, 2016)
- 하지만, 실제로 여기서 소개되는 3가지의 공격 방법에는 위의 모델은 유효하지 않다.
에 해당하는 새로운 새로운 공격방법을 소개하고자 한다.
- Defense를 평가하는데에는 2가지 방법이 있다.
- Robustness에 대한 증명을 만든다:
정확하게 구현해내기는 어렵지만, 대략적인 값을 구할 수 있다. - Constructive한 공격을 보여준다:
이 논문에서 사용하는 방법이다.
- Robustness에 대한 증명을 만든다:
Previous Attack Algorithms
- L-BFGS(Box constrained)
Attack
- FGSM(Fast Gradient Sign Method)
Attack
- JSMA(Jacobian-based Saliency Map Attack)
Attack
- Deepfool
Attack
- L-BFGS보다 낫다.
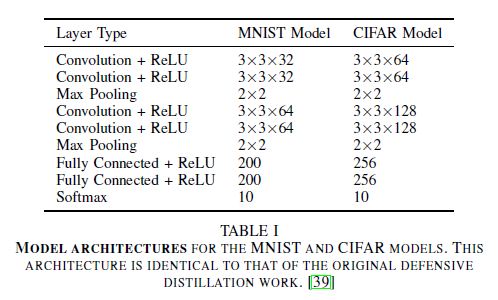
Model Setup
- Architecture
- Defensive distillation의 구조와 동일하다.
- momentum-based SGD optimizer를 이용한다.
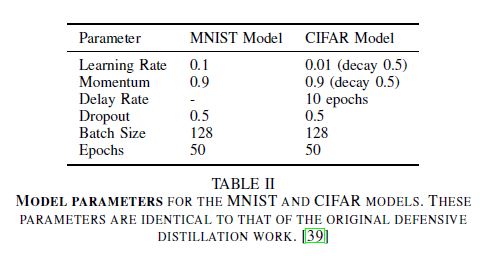
- Parameter
- Defensive distillation의 parameter와 동일하다.
- Dataset
- 두개의 network를 MNIST와 CIFAR-10로 train한다.
- 한개의 ImageNet에 대해 미리 train된 network를 사용한다.
- MNIST와 CIFAR-10이 ImageNet에 비해서 상대적으로 작은 dataset이기 때문에 이를 추가적으로 이용한다.
- 대신, 미리 train된 Inception v3 network를 이용한다.
Approach
- 거리를 최소화 하는
를 찾으려 한다.
- minimize
(distance metric)
such that
- 이를 해결하기는 굉장히 어렵기 때문에 difficult한 constraint를 objective function으로 바꾼다.
- minimize
- Objective Function:
if and only if
을 만족하는
를 objective funtion이라 한다.
- objective function은 아래와 같이 다른 방식들로 표현될 수 있다.
- 이를 이용하여 문제를 직접적으로 해결하는 대신, 변형된 형태인 아래의 문제를 해결 하도록 한다.
(given, find
that solves)
- minimize
such that«««< HEAD:summary/Towards Evaluating the Robustness of Neural Networks.md
- minimize
-
이 때의
의 값은 가장 효과적이라 판명된
를 토대로 찾은 값을 이용한다.
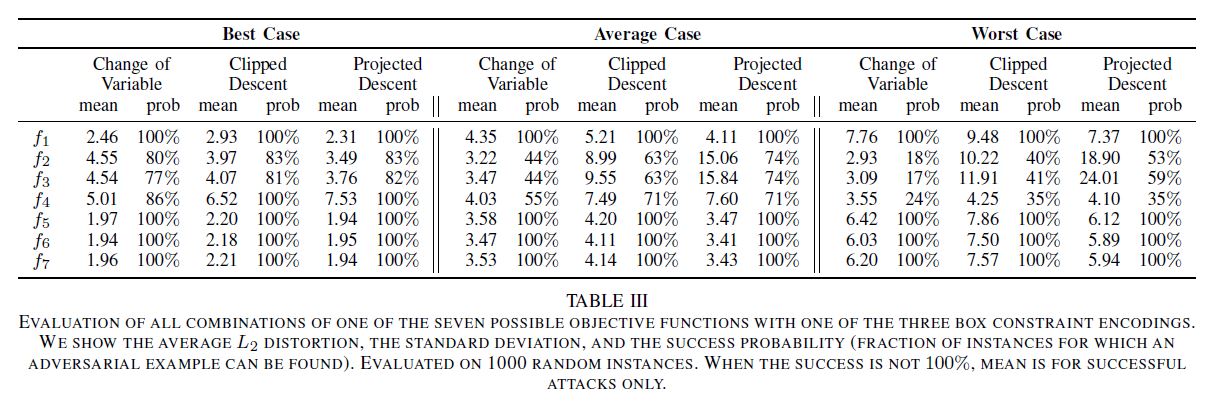
- 아래의 표를 통해서 가장 효과적이라고 보이는 objective function을 선택한다.
의 값은 가장 효과적이라 판명된
를 토대로 찾은 값을 이용한다.
- Box constraints
- modification이 유효한 이미지를 생산하기 위해서,
를 모든
에 대해서 만족해야 한다.
- 이는 아래의 세가지 방법으로 만족시킬 수 있다.
- Projected gradient descent
- 복잡한 update step을 갖는 Gradient Descent approach에는 잘 적용되지 않을 수 있다.
- Clipped gradient descent
를
로 대체하여 사용하는 방식이다.
- Change of variables
- 새로운 변수
를 소개한다.
- 정의된
를 최적화 하는 대신,
를 이용하여
을 이용해서에 대한 최적화를 한다.
- 새로운 변수
- Projected gradient descent
- modification이 유효한 이미지를 생산하기 위해서,
Three Attacks
 Attack
Attack
- Method
- minimize
withdefined as
- 먼저 찾은 objective function에 기반한다.
- minimize
- Attack Applied to MNIST
 Attack
Attack
- Method
- 분류 결과에 영향을 많이 끼치지 않는 픽셀을 찾아내고 값을 고정한다.
- 고정되는 픽셀의 수가 늘어남에 따라서 분류된 남은 픽셀들을 modify하여 adversarial example을 만들어낸다.
- 고정되는 픽셀은 반복 과정에서
Attack을 이용하여 구할 수 있다.
- 고정되는 픽셀은 반복 과정에서
- Attack Applied to MNIST
 Attack
Attack
- Method
distance metric이 항상 미분이 가능한 것이 아니므로, naive한 최적화를 통해서 결과를 얻으려 했다.
- 하지만, gradient descent가 빠르게 두 지점 사이에서 진동하게 되어 결과값은 좋지 않았다.
- 해결책
- iterative attack을 이용, 각 iteration이 끝날 때 마다
를 최소화 한다.
- 각각의 iteration 에서 만약
이라면,
의 값을 줄이고 다시 반복을 한다.
- 이때
의 값도 잘 설정되어야 한다. 이는
Attack에서의 방법과 동일하다.
- iterative attack을 이용, 각 iteration이 끝날 때 마다
- Attack Applied to MNIST
Evaluating Attacks
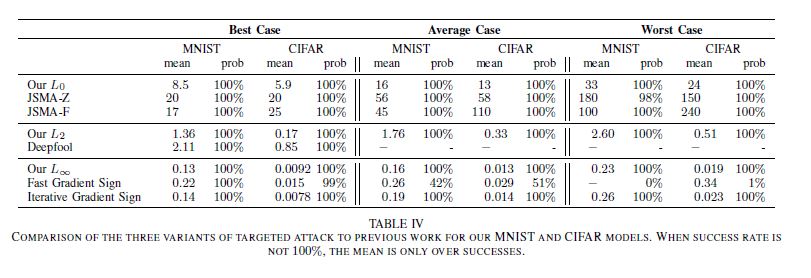
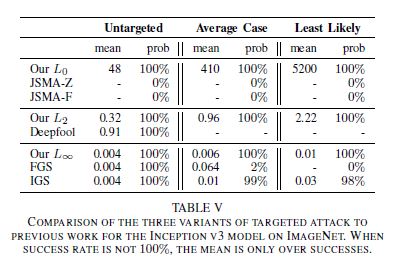
- Compared to previous Attacks
Evaluating Defensive Distillation
Defensive Distillation
- Neural Network의 robustness를 증가시키기 위해서 distillation을 사용한다.
- 차이점
- Teacher model과 distilled model 모두 같은 사이즈를 지닌다.
- Defensive distillation은 예측에 있어서 confidence를 올리기 위해 큰 distillation temperature를 이용한다.
- Softmax function을 변형하여 이용하며 temperature 변수
를 이용한다.
- 4 step에 따라 진행된다
- softmax의 temperature를 training phase동안
로 설정해서 teacher network를 train한다.
- Soft label들을 training set의 각 instance에 apply해서 계산한다. 이때 softmax의 temperature는
이다.
- Distilled network를 train하는데 이 network의 모양은 teacher network와 동일하다. 이때 softmax의 temperature는
이다.
- 마지막으로, Distilled network를 test할 때 temperature를 1로 설정한다.
- softmax의 temperature를 training phase동안
기존의 Attack의 Fragility
- L-BFGS와 Deepfool은
의 gradient가 거의 항상 0의 값을 가졌기 때문에 실패하였다.
- JSMA-F의 경우에는 L-BFGS와 같은 이유로 실패하였다.
의 layer가 매우 커서 softmax가 hard maximum이 되어버리기 때문이다.
- JSMA-Z의 경우에는 JSMA-F와는 완전 다른 이유로 실패한다.
를 이용하기 때문에 gradient vanishing의 잠재적인 issue를 없앤다. 하지만, distillation을 공격하는데 사용하지 않기 때문에 fail한다.
- FGSM은 L-BFGS와 같은 이유로 실패하였다.
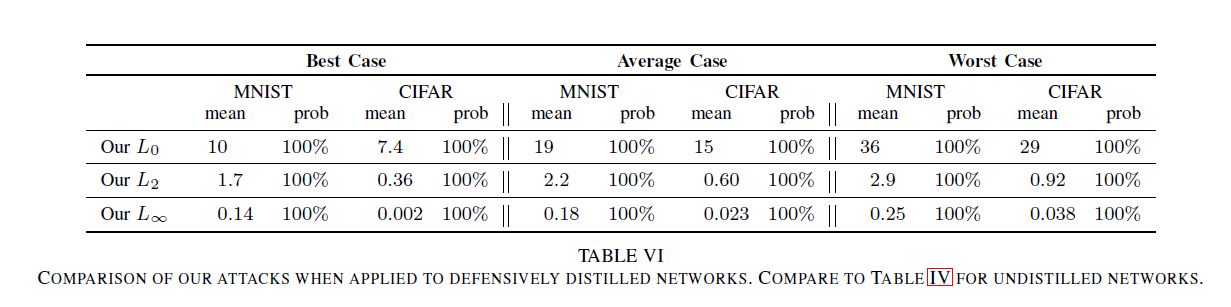
Applying New Attack
- Distillation이 marginal value를 제공하는 것을 발견했다.
- Table IV와 비교해서 distillation이 거의 영향을 끼치지 않은것을 확인할 수 있었다.
와
Attack은 살짝 성능이 떨어졌고,
Attack은 거의 똑같이 작동하는 것을 확인할 수 있었다.
- 공격의 성공률은 100%임을 확인할 수 있었다.
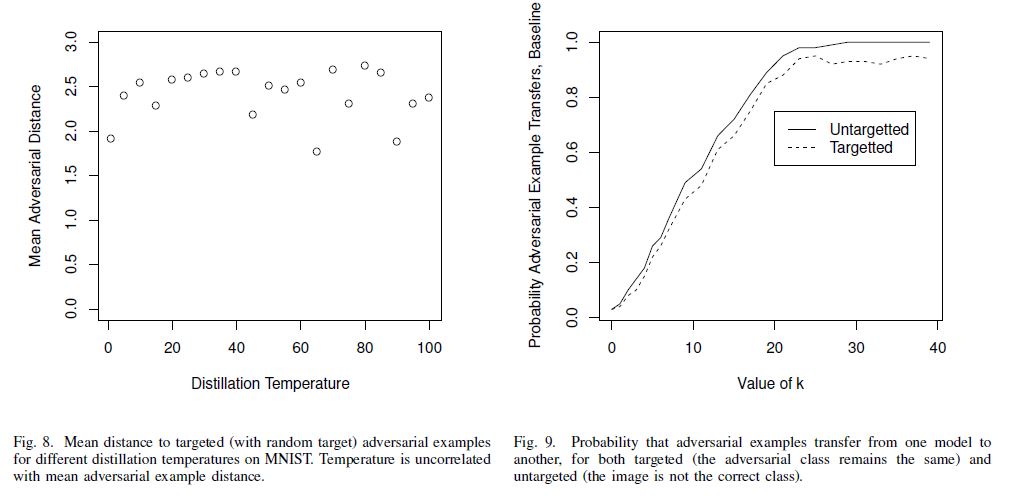
Effect of Temperature
- Distillation에서의 temperature의 증가는 robustness를 증가시키지 않는다.
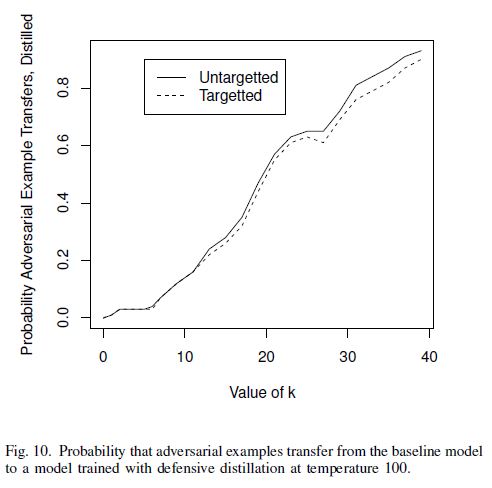
Transferability
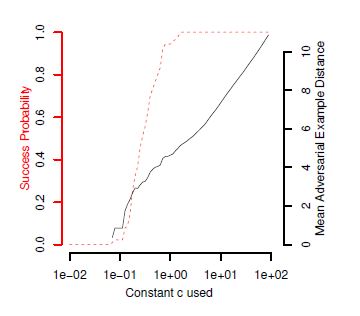
- MNIST에서의
attack의 loss function 변수
가 증가함에 따라 transferability의 성공률이 linear하게 증가함을 확인했다.

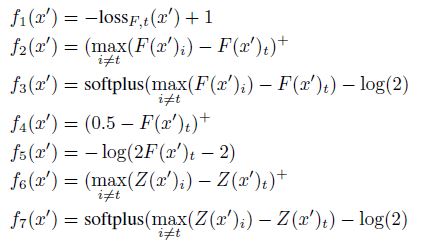



댓글남기기